Numerical Linear Algebra Group

President HRH Duke of Edinburgh presenting honorary fellowship of The Institute of Mathematics and its Applications to James Wilkinson in 1977 (© The IMA).

The title of this post is the same as that of a symposium organized by Michael J. D. Powell and the Institute of Mathematics and its Applications (IMA) at the Royal Society in London on July 6th, 1977. The meeting commemorated the election of James Hardy Wilkinson to an Honorary Fellowship of the IMA.

The proceedings of the meeting were published by the IMA in a 91-page A5 booklet. As far as I am aware, few copies of the booklet survive and its contents have not previously been made available online. I am grateful to David Youdan, Executive Director of the IMA, for giving me permission to provide here a scan of the booklet. It is timely to do so, because this year marks the 100th anniversary of the birth of Wilkinson.

• The full booklet (31Mb).

Here are the individual chapters, with comments from Mike Powell’s preface in quotes.

• About Jim Wilkinson, with a Commemorative Snippet on Backward Error Analysis, L. Fox (Oxford University Computing Laboratory). “Leslie Fox describes many of Jim Wilkinson’s achievements that have not been published before and he exposes the accuracy of some ill-conditioned least squares calculations.”
• Inverse Iteration, Newton’s Method, and Non-linear Eigenvalue Problems, M. R. Osborne (Australian National University). “Mike Osborne unifies the convergence properties of a main class of iterative methods for calculating eigenvalues.”
• A New Look at Error Analysis, C. W. Clenshaw (University of Lancaster). “Charles Clenshaw develops an idea, due to Frank Olver, for treating the accumulation of errors in floating point arithmetic.”
• A Problem in Numerical Linear Algebra, J. H. Wilkinson (National Physical Laboratory). “Jim Wilkinson shows the relevance in practice of the equivalence of repeated matrix eigenvalues, the ill-conditioning of the matrix eigenvector calculation, and the orthogonality of left and right hand eigenvectors that have a common eigenvalue.”

For more information about Wilkinson, see this web page that Sven Hammarling and I have created.

by Sven Hammarling and Nick Higham

We collect here some quotes from the work of Jim Wilkinson. These reflect his unique perspective as a mathematician who was involved in designing and building one of the first digital computers and who subsequently developed and analyzed a variety of numerical algorithms

We have arranged the quotes under the following headings:

Program libraries | Floating-point arithmetic | Rounding error analysis | Conditioning | Backward error analysis | Polynomials | Interaction on Pilot ACE | Communication avoidance | Linear algebra on Pilot ACE

by Sven Hammarling and Nick Higham

It is often thought that Jim Wilkinson developed backward error analysis because of his early involvement in solving systems of linear equations. In his 1970 Turing lecture [5] he described an experience, during world war II at the Armament Research Department, of solving a system of twelve linear equations on a desk computer, using Gaussian elimination. (He doesn’t say how long it took, but it must surely have been several days.) The coefficients were of order unity and, using ten decimal digit computation, he found that the coefficients of the reduced equation determining had four leading zeros, so he felt that the solutions could surely have no more than six correct figures. As a check on his calculations, he then computed the residuals and to his surprise the left hand sides agreed with the right hand sides to the full ten figures.

A slide of Wilkinson’s describing the solution of the system of 18 equations.

After the war Wilkinson joined the Mathematics Division at the National Physical Laboratory. Soon after his arrival, a system of eighteen equations were given to the Mathematics Division. This required a joint effort, which was manned by Leslie Fox, Eric Goodwin, Alan Turing and Wilkinson. Again, the solution was somewhat ill conditioned, as revealed by the final reduced equation, but again in computing the residuals the right and left hand sides agreed to full accuracy. Incidentally, Wilkinson and his colleagues used iterative refinement, which convinced them that the first solution had been accurate to six figures.

These experiences did not straightforwardly lead Wilkinson to develop backward error analysis. In [7] he says that he first used backward error analysis in connection with simple programs for computing zeros of polynomials soon after PILOT ACE came into use, specifically a program for evaluating a polynomial by nested multiplication and a program for carrying out polynomial deflation. But he nevertheless did not recognise backward error analysis as a general tool. Wilkinson explains

It is natural to ask why I did not immediately set about using this type of error analysis as a general purpose tool. In retrospect it seems amazing that I did not try it on Gaussian elimination and on various eigenvalue algorithms in which I was keenly interested at the time. The truth is that it did not occur to me for one moment to do so.

His explicit recognition of a tool that he decided to call backward error analysis soon came through his experience of solving eigenvalue problems on PILOT ACE. He states further in [7]:

Because of the small storage capacity of the PILOT ACE virtually the only algorithm that could be used for dealing with large unsymmetric eigenvalue problems was the power method supplemented by various techniques for accelerating convergence. After each eigenvalue/eigenvector was determined this pair was removed by deflation. Now at that time deflation was generally held to be extremely unstable and accordingly I used it at first with great trepidation. However, it soon became evident that it was being remarkably effective.

As with the linear equation problem, Wilkinson computed residuals, , where and are the computed values, with normalised so that , and, even after many deflations, he found that the residuals were remarkably small. He then realised that

and this led him directly to the backward error analysis since, if we put 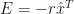, then and are an exact eigenvalue and eigenvector of the matrix 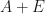. He now recognised that the process could be widely used and this, of course, led to his 1963 book Rounding Errors in Algebraic Processes [3] and, soon after, to The Algebraic Eigenvalue Problem [4].

It should be noted that Wilkinson did not claim to be the first to perform a backward error analysis. He attributes the first analysis to von Neumann and Goldstine in their 1947 paper [2], which, as Wilkinson said in his von Neumann prize paper “is not exactly bedtime reading” [6]. Wilkinson also gives great credit to Givens for his backward error analysis of orthogonal tridiagonalisation in his, sadly, unpublished technical report [1].

References

[1]   W. Givens. Numerical computation of the characteristic values of a real symmetric matrix. Technical Report ORNL-1574, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA, 1954.

[2]   J. von Neumann and H. H. Goldstine. Numerical inverting of matrices of high order. Bull. Amer. Math. Soc., 53:1021–1099, 1947.

[3]   J. H. Wilkinson. Rounding Errors in Algebraic Processes. Notes on Applied Science, No.32. HMSO, London, UK, 1963. (Also published by Prentice-Hall, Englewood Cliffs, NJ, USA, 1964. Reprinted by Dover Publications, New York, 1994).

[4]   J. H.Wilkinson. The Algebraic Eigenvalue Problem. Oxford University Press, Oxford, UK, 1965.

[5]   J. H. Wilkinson. Some comments from a numerical analyst. J. ACM, 18:137–147, 1971. (The 1970 A. M. Turing lecture).

[6]   J. H. Wilkinson. Modern error analysis. SIAM Review, 13:548–568, 1971. (The 1970 von Neumann lecture).

[7]   J. H. Wilkinson. The state of the art in error analysis. NAG Newsletter, 2/85:5–28, 1985. (Invited lecture for the NAG 1984 Annual General Meeting).